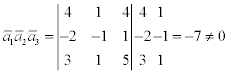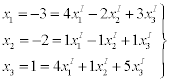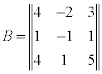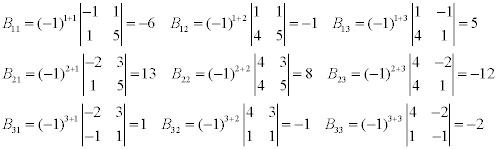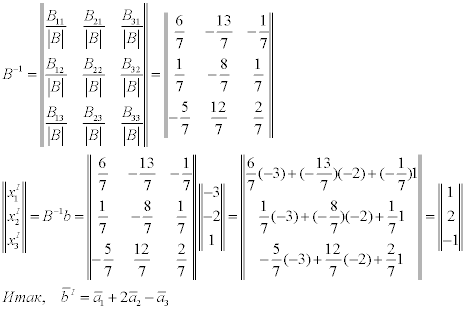1. Дано: 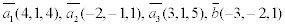
Записать вектор 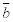 в базисе векторов в базисе векторов 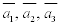 . . Решение:
Чтобы векторы образовывали базис нужно, чтобы они были некомпланарны, т.е. их векторное произведение (объем параллелепипеда на векторах) не равнялось нулю. 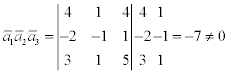
Вектор в старом базисе:
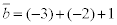
В новом:
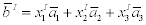
Старые координаты связаны с новыми 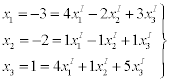
Решив эту систему с помощью обратной матрицы, найду координаты вектора 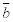 в новом базисе в новом базисе 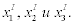
Матрица, связывающая старые и новые координаты:
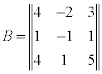
Новые и старые координаты связаны отношением:
b=BbI
b
– матрица старых координат;
B
– матрица, связывающая координаты старые и новые; BI – матрица новых координатОтсюда:
bI=B-1b>
Найду
обратную матрицу B-1.
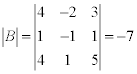
Определитель 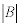 ≠0 , значит обратная матрица существует. ≠0 , значит обратная матрица существует.
Найду алгебраические дополнения:
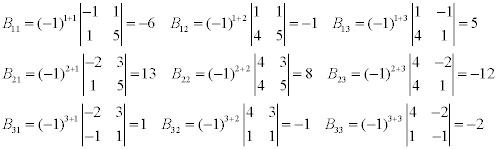
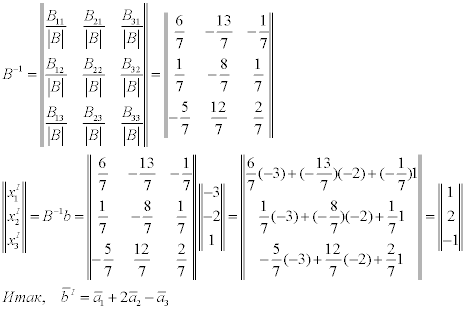
|